[Deep Learning Specialization] Deep Neural Networks - week4:: seoftware

📜 강의 정리 

* Coursera 강의 중 Andrew Ng 교수님의 Deep Learning Specialization 강의를 공부하고 정리한 내용입니다.

* 영어 공부를 하려고 영어로 강의를 정리하고 있습니다. 혹시 틀린 부분이나 어색한 부분이 있다면 댓글로 알려주시거나 넘어가주시면 감사하겠습니다

---

Deep Neural Networks

 

1. Forward propagation in a Deep Network

We can represent each layer as follow

• Z[l] = W[l]@A[l-1] + b[l] 
• A[l] = g[l](Z[l]) (l = layer)

In vectorizing process, we have no choice but to use explicit for loop to compute above formula in every layers. 

2. Getting your matrix dimensions right

When implementing a deep neural network, I am often confused about dimensions of weights. 

• Dimension of W : (out_features, in_features)
• Dimension of b : (out_features, 1)
• Dimension of dw : (out_features, in_features)
• Dimension of db : (out_features, 1)

Vectorized Version

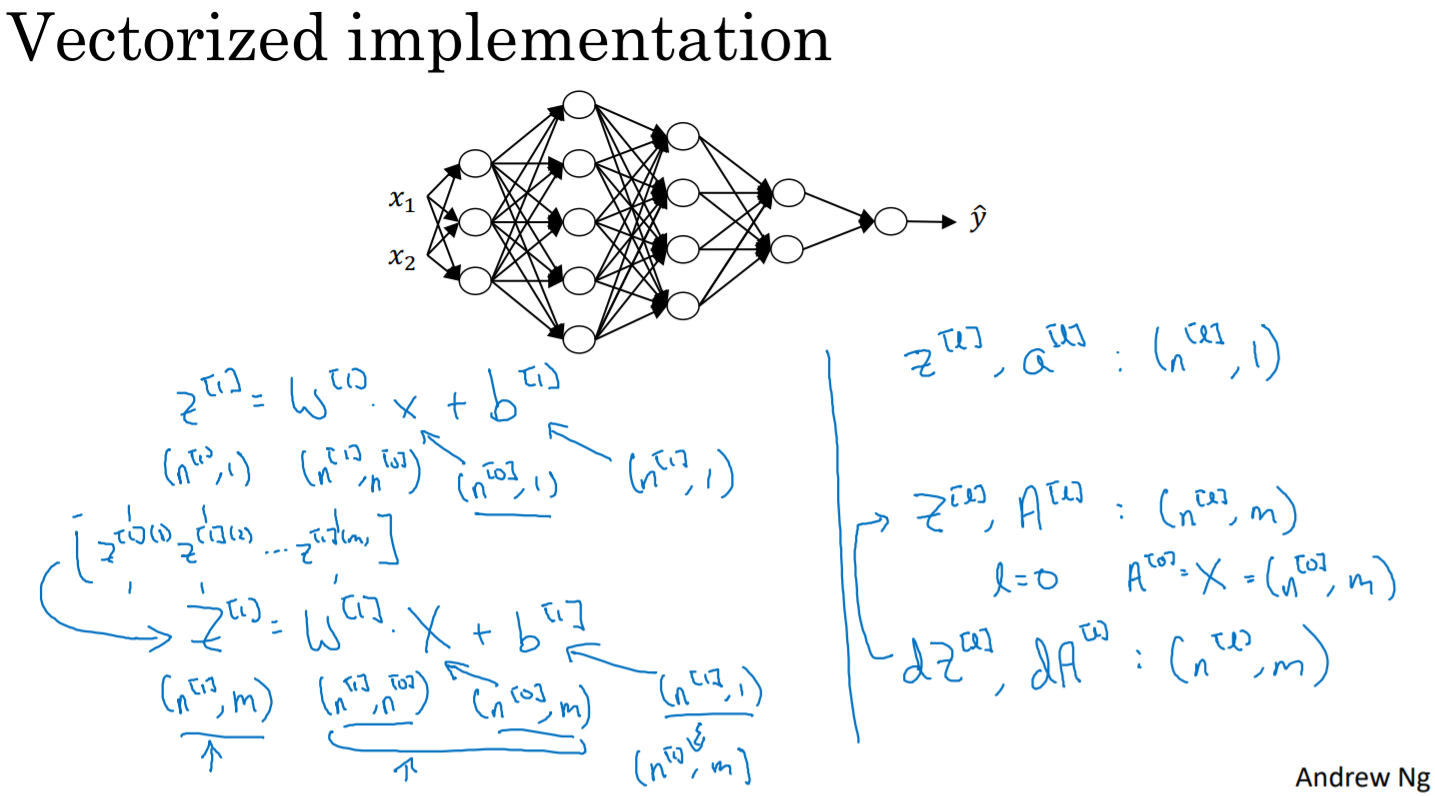
Just extend 1 to m(number of training examples) in X and Z when you represent vectorized implementation.

The shape of b is still (n, 1) because it is duplicated into (n, m) matrix by python broadcasting and then added element-wise. 

One point is that the dimension of each parameter is same as before dimension.

 

3. Why Deep representation?

Every layers are different functions to extract features. For example, face recognition, the network can extract horizontal or vertical features in the first layer and each can be concentrated each part like nose or eyes in the second layer. 

The deeper layers of nn are typically computing more complex features of the input than the earlier layer.

4. Building Blocks of Deep Neural Network

In each layer there's a forward propagation step and there's a corresponding backward propagation step. 

And has a cache to pass information from one to the other. 

In a cache, there are Z, W, b parameters for computing gradients

5. Parameters & Hyperparameters

• Parameters : W[l], b[l] (l = 1, ..., L)
• Hyperparameters : learning rate, #iterations, #hidden layers L, #hidden units n[l], choice activation function, momentum, regularization, mini batch size etc.

6. derivatives formula

$d Z^{[L]}=A^{[L]}-Y$
$d W^{[L]}=\frac{1}{m} d Z^{[L]} A^{[L-1]^{T}}$
$d b^{[L]}=\frac{1}{m} n p . s u m\left(d Z^{[L]}\right.$, axis $=1$, keepdims $=$ True $)$
$d Z^{[L-1]}=W^{[L]^{T}} d Z^{[L]} * g^{\prime[L-1]}\left(Z^{[L-1]}\right)$
Note that * denotes element-wise multiplication)
$d Z^{[1]}=W^{[2]} d Z^{[2]} * g^{\prime[1]}\left(Z^{[1]}\right)$
$d W^{[1]}=\frac{1}{m} d Z^{[1]} A^{[0]^{T}}$
Note that $A^{[0]^{T}}$ is another way to denote the input features, which is also written as $X^{T}$
$d b^{[1]}=\frac{1}{m} n p . s u m\left(d Z^{[1]}\right.$, axis $=1$, keepdims $=$ True $)$