📜 강의 정리
* Cousera 강의 중 Andrew Ng 교수님의 Deep Learning Specialization 강의를 공부하고 정리한 내용입니다.
* 영어 공부를 하려고 영어로 강의를 정리하고 있습니다. 혹시 틀린 부분이나 어색한 부분이 있다면 댓글로 알려주시거나 넘어가주시면 감사하겠습니다
1. Neural networks overview
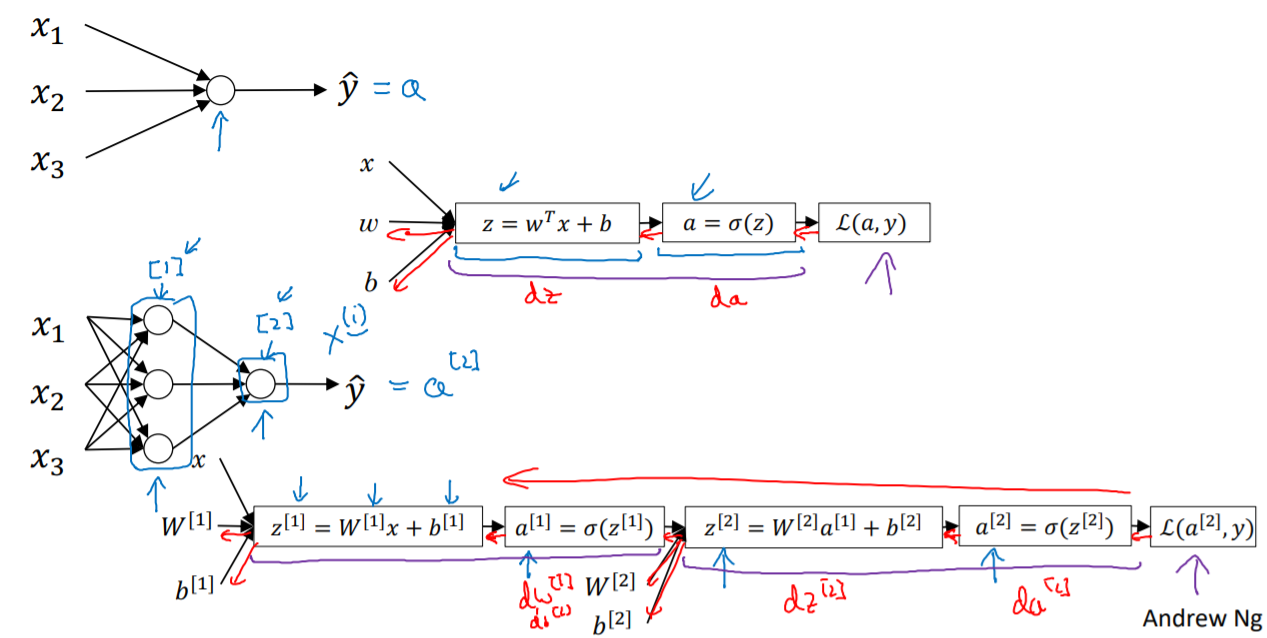
I learned about new notations and representation of above shallow neural network. Brackets [] means the layer order and x superscript (i) means i-th training example of x.
2. Neural network representation
We can represent input layer x to a^[0], called layer zero, so technically, there are three layers in a "two layered neural network".
Two layered neural network consists of...
- Input layer a^[0]
- Hidden layer a^[1] (including W^[1], b^[1])
- Output layer a^[2] (including W^[2], b^[2])
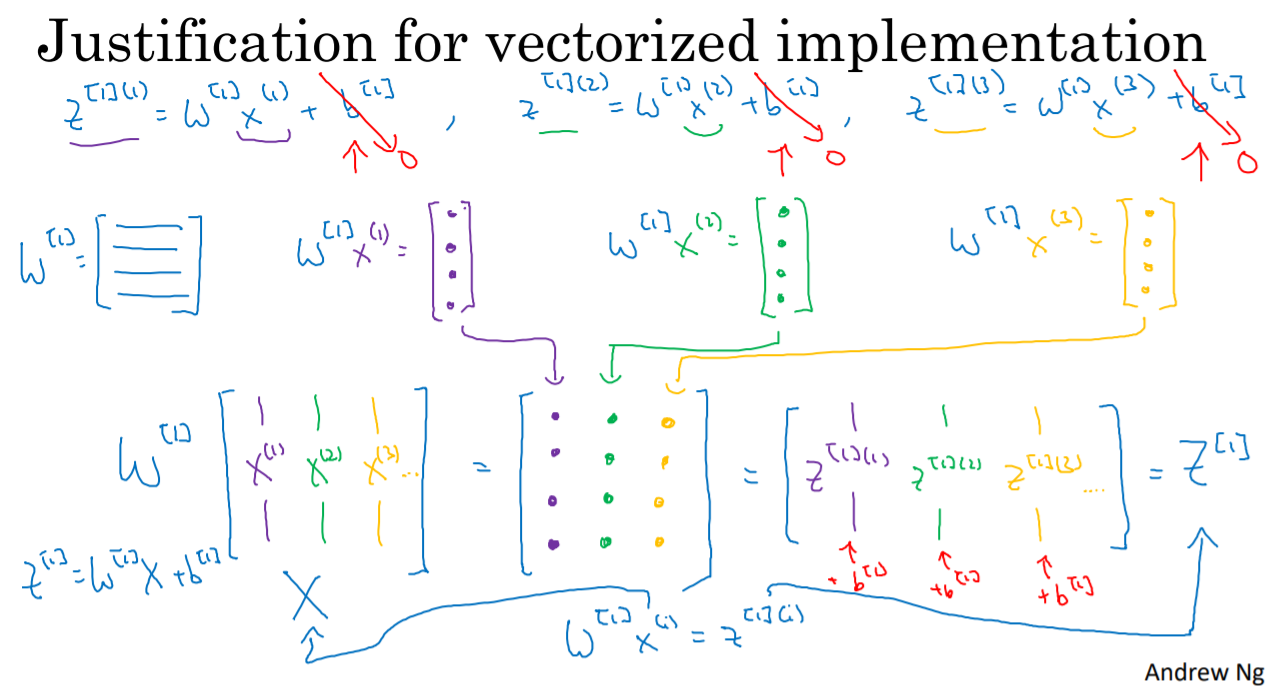
3. Vetorizing Across Mutiple Examples
4. Activation functions
- Sigmoid function
- the tanh is pretty much strictly superior.
- Derivatives : g'(z) = g(z)(1-g(z))
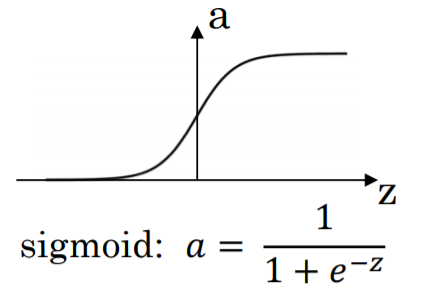
- tanh

- Derivatives : g'(z) = 1-(g(z))^2
- ReLU
- Leaky ReLU

5. Why do you need Non-Linear function?
Z[1] = W[1]*x + b[1]; A[1] = Z[1]
Z[2] = W[2]*A[1] + b[2]= W[2]*W[1]*x + W[2]b[1] + b[2] = W'x + b'
"W'x + b'" is a linear function. If you don't have an activation function, then no matter how many layers your neural network has, all it's doing is just computing a linear activation function. So you might as well not have any hidden layers.
6. Derivatives of Activation Functions
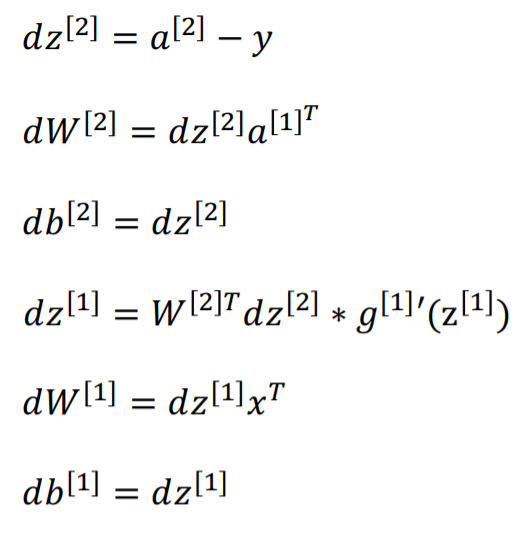





댓글